Time Warp--On Science--On Health-- On Defense-- Artcam

About The Author

Dr. Mantravadi is an optical scientist and engineer. He has held teaching posts worldwide and has done research in optics and holography. He holds several patents and has written a number of papers in the general areas of optics and holography. The Murty Interferometer is named in his honor.
Note: The author used the name M.V.R.K Murty in most of his publications. (AW)

PRIMARY RAINBOW

Most people must have observed rainbows at some time or other. A rainbow is formed either in the morning time or evening time when the sun is above the horizon but not too high. Also it is necessary that the atmosphere contain droplets of water. This usually happens when it is about to rain, during the rain or immediately after the rain. The droplets of water hanging in the air are of spherical shape.

The sun subtends an angle of 30' of arc and hence for the purpose of simple analysis, may be considered to be a source of collimated white light.

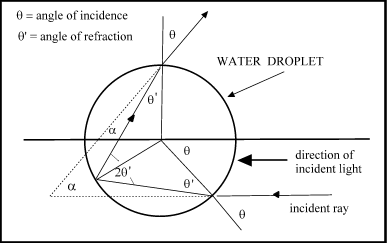
Let us consider a simple spherical drop of water and assume that light from the sun is impinging on the droplet. Thus the droplet is receiving a collimated beam equal to its diameter. The angle of incidence on the surface of the spherical droplet varies from 0º to 90º.

Let us consider a ray making an angle at some point on the droplet. This is shown in Figure 1. The ray is refracted and the angle of refraction is '. Then the ray is reflected once and then emerges out of the droplet as shown. The angle between the incident direction and the emerging direction is denoted by

Figure 1

Using the geometry of the Figure, we can show that

=(4' - 2)(1)

Since both and ' are varying as the position of the ray, can have a maximum value. This occurs when

d/d=0.

Hence,

d/d=4(d'/d) - 2=0. (2)

We know that sin=nsin' by the law of refraction where n is the refractive index of water which is taken as 1.333.

Hence,

d'/d=cos/ncos'. (3)

We can transform Equation 3 as follows:

cos/ncos'=(1 - sin) / n(1 - sin')

=((1 - sin) / (n - sin))(4)

Hence

4(1 - sin) / (n - sin)=2

or,

sin=(4 - n)/3

Which reduces to

sin=((4 - n)/3))(5)

Thus using n=1.333, we have

sin=0.8608

and

=59.41 º

'=40.22 º

Hence =42.08 º (6)

Since around the maximum value of , the rays of light bunch together and hence the intensity is very high. Now since the index of refraction of water is also a function of wavelength of light, the index for blue is higher than 1.333 and for the red it is lower than 1.333. Thus the value of is lower for the blue and higher for red. Thus around the angle of 42.08 º the for blue is smaller and higher for red.

If we assume that the sphere of water is rotated about the incident direction, we get the full trace of the rays of light. Thus the rays around the angle =42.08º describe a full circle. The outer circle will be red and the inner circle will be blue.

Now the person sees the rainbow because there is a large collection of water drops in the air in front of him and he gets rays of light from all possible directions from all drops of water.

Why can't we see the full circle of the rainbow? Let us assume that the sun is at the horizon (at sunrise or sunset). Thus the uppermost part of the rainbow is at an elevation of 42.08º. The lower part of the rainbow is below the horizon and hence cannot be seen. As the sun rises above the horizon the upper part of the rainbow comes lower and lower and disappears when the sun reaches an elevation of 42.08º.

SECONDARY RAINBOW

The discussion in the preceding section was that of a rainbow formed by one reflection inside the water drop. This rainbow is called a 'primary rainbow'. A weaker second rainbow is sometimes seen under optimal conditions. This is called a secondary rainbow and is attributable to the light reflected two times inside the water droplet. This rainbow is much weaker.

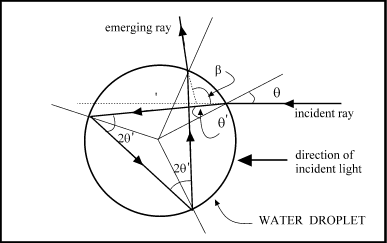
Similar type of analysis can be made to find the angle at which this is seen. Figure 2 shows the circle representing the water droplet where the ray is reflected twice inside before emerging from the droplet. We shall call the angle made by this ray with the incident direction .

Figure 2

We can show that

=180º - 6' + 2(7)

Using similar arguments as before, the direction in which the light emerges with greatest intensity is obtained by solving

d/d=0

Hence,

d/d=2 - 6d'/d=0

and as before, we have

d'/d=cos/ncos'

Going through the same exercise, we have the solution

sin=((9 - n)/8) (8)

As before for n=1.333,

=71.84º

'=45.47º

=50.89º

It is interesting to point out that this angle is minimum while for the primary rainbow, is maximum.

It is easy to see this by the following simple argument. can vary between the limits of 0º and 90º.

When

=0º=0º =180º

and, when

=90º=14.43º =68.36º

Thus (42.08º) is higher than the two limits of 0º and 14.43º while (51º) is lower than the two limits 180º and 68.36º. Because of this, the sequence of colors is reversed in the secondary rainbow, i.e., the red is inside and the blue outside.

IS IT POSSIBLE TO OBTAIN A FULL CIRCLE RAINBOW IN NATURE?

As discussed before, the rainbow as seen at ground level is only part of a circle. It should be possible to see a full circle rainbow under very special circumstances. I am not sure how many people have seen this phenomena while on an airplane when the sun is close to the zenith. If at that time the atmosphere below is filled with rain drops, it is possible to see the major portion of the full circle rainbow. I have not seen it myself. But it is possible that some of you may have seen it or even photographed it.

EXPERIMENT WITH A LAWN SPRINKLER

We can create in a limited space a fine suspension of water droplets by the use of a sprinkler which sprays a fine mist of water into the air. If this is done outdoors (recommended), we can see a very nice rainbow when the sun is above the horizon (morning or afternoon) with the sun behind and the sprinkler in front. If one is near a large waterfall creating spray, one can see the rainbow against the background of the fall when the sun is at the right elevation. This phenomenon is sometimes spectacular at places like Niagara Falls.

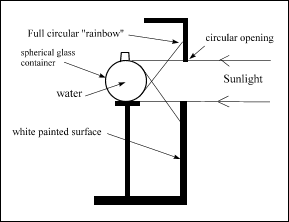
EXPERIMENT WITH A SINGLE LARGE SPHERE OF WATER

We can obtain a transparent spherical container and fill it with water. (A plastic sphere can usually be found in plastic supply stores). The sphere of water is held in a suitable box as shown in Figure 3. In the front of the box a hole about the same size as that of the sphere is made to allow the sunlight to pass through and impinge on the sphere. Note that the sphere is positioned with a platform so that it is centered with respect to the hole.

Figure 3

When sunlight is directed to the sphere, a full circle "rainbow" is seen projected on the inside surface of the box around the hole.

© 1996 Murty V. Mantravadi

Dr. Mantravadi can be reached by filling out our feedback form and referencing this article.

Homepage | More Perspectives on Science | Armchair World Directory

We appreciate any comments or questions you might have. Our e-mail address is .

© Copyright 2001-2003 Armchair World